
A Universal Description of Stochastic Oscillators
Many natural systems exhibit oscillations that show sizeable fluctuations in frequency and amplitude. This variability can arise from a wide variety of physical mechanisms, so theoretical descriptions of these phenomena have been made on a case-by-case basis. In a paper published in the Proceedings of the National Academy of Sciences, a team of interdisciplinary scientists from the Universidad Complutense in Madrid, Humboldt University and the Bernstein Center for Computational Neuroscience in Berlin, and the Ecole normale supérieure-PSL in Paris, develop a general theory for stochastic oscillators, based on a canonical nonlinear transformation of variables.
What do the beating of the human heart, the flashing of fireflies in a field, and the swinging of children on a playground have in common? They are all examples of rhythmic processes – oscillations – that occur spontaneously. Oscillations can be found everywhere, and arise from many different physical, chemical, or biological mechanisms.
Most oscillations are “noisy” or irregular, to a greater or lesser extent. For example, the heart rhythm is not 100% regular. A natural variation of 5-10% in the heart beat is considered healthy.
Because they arise from a myriad of different underlying mechanisms – called “bifurcations” by theoretical physicists – the theoretical descriptions of these phenomena have been scattered. Physicists have understood different kinds of oscillations on a case-by-case basis.
An interdisciplinary team with expertise spanning physics, neuroscience, and mathematics have introduced a new “universal description” of stochastic oscillators. The new work uses complex numbers to describe both the timing of oscillators, and how noisy, or imprecise in their timing, they are. The scientists’ invention makes it possible to compare oscillators that were previously considered to have completely different properties.
One of the study’s authors, applied mathematician Peter Thomas from Case Western Reserve University in Cleveland, Ohio, explains: “If a small particle – like a protein molecule in a living cell – is held in place by the stuff surrounding it, then it won’t oscillate on its own. But if it is bombarded by even smaller particles – like water molecules – it will get knocked a little out of position. Then the elastic surrounding will pull it back, but the water will keep pushing it away. It ends up jiggling back and forth. You wouldn’t think this process could be compared with, say, the pendulum on a grandfather clock, but they are both oscillators. And our new formalism lets you compare them, apples-to-apples.”
At the heart of the study is a mathematical transformation to a new variable, that strikingly simplifies the description. As physicist Benjamin Lindner from Humboldt University in Berlin Germany, last author of the study, puts it, “Noisy oscillators are characterized by their temporal correlation, by their response to an external forcing, and by the way they interact if coupled to other oscillators. If we look at the system through the transformed variable, these characteristics follow very simple and exact formulas - there is no approximation involved.”
“What makes this work so exciting is that oscillations are everywhere, once you know what to look for,” says computational neuroscientist Boris Gutkin from Ecole normale superieure. “From satellites going around the earth to the synchronization of fireflies in a tree, to brain rhythms that kick up when we comprehend language, we have found a truly universal description of stochastic oscillators.”
The study’s lead author, Alberto Perez-Cervera, an applied mathematician from Universidad Complutense de Madrid, says “The mathematical transformation we put forward in the paper acts as a lens through which we invite the reader to observe noisy oscillators. We expect the reader to enjoy the striking experience of observing how different and, a priori, complex phenomena become comparable and categorized under simple, but still meaningful, universal mathematical forms when observed through our lens.”
(*) A mathematical transformation is when you change the variables in the problem from original ones to another using some function and the new variables are much easier to work with.
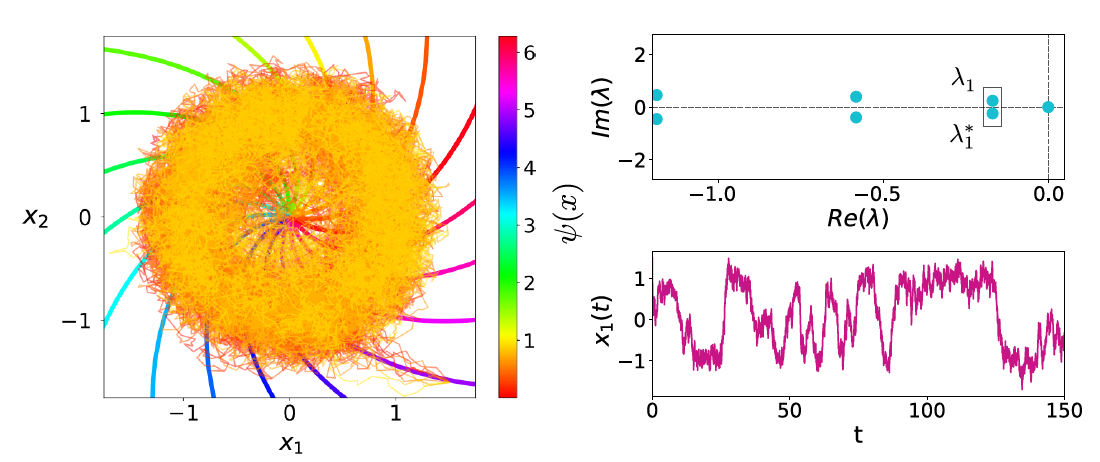
Alberto Pérez-Cervera, Boris Gutkin, Peter J. Thomas and Benjamin Lindner (2023). A universal description of stochastic oscillators. PNAS, 120 (29) e2303222120. doi:10.1073/pnas.2303222120.
Contact:
Boris Gutkin, Directeur de recherche CNRS
Laboratoire de Neurosciences Cognitives et Computationnelles (Inserm, ENS-PSL)
boris.gutkin@ens.psl.eu



